We provide effective and economically affordable training courses for R and Python, Click here for more details and course registration !
The normality assumption in linear regression is necessary to ensure the estimates of parameters are unbiased and the hypothesis testing is correct. It states that for the fixed or given values of explanatory variables, the dependent variables are normally distributed around the mean 0. It is equivalent to say that the residuals after model estimation follow a normal distribution with the mean 0.
The ‘car’ package in R provides various methods for diagnosing linear regression, among which is the function qqPlot(), which can be used for assessing normality assumption. If the residuals vs. the theoretical quantiles all stay randomly on the diagonal straight line, we can say the normality assumption is met.
In this post we show how to implement this function in RStudio with two example codes.
The first example is of analyzing murder rates as a couple of social demographic independent variables for all states in USA.
#load library 'car'
library(car)
#to create a data frame of 5 column variables, from state.77
#dataset in R
st_US <- as.data.frame(state.x77[,c("Murder", "Population",
"Illiteracy", "Income", "Frost")])
#show the data frame
st_US
#carry out a linear regression analysis, with Murder as
#dependent variable, and rest of variables as independent
#variables in data frame st_US
murder_fit <- lm(Murder ~ Population + Illiteracy + Income + Frost, data=states)
#using qqPlot
#id=list(method="identify") allows interactive analysis with # the plot
#simulate=TRUE provides a 95% confidence range around the
#straight line
qqPlot(murder_fit, simulate=TRUE, labels=row.names(states),
id=list(method="identify"), main="Q-Q Plot")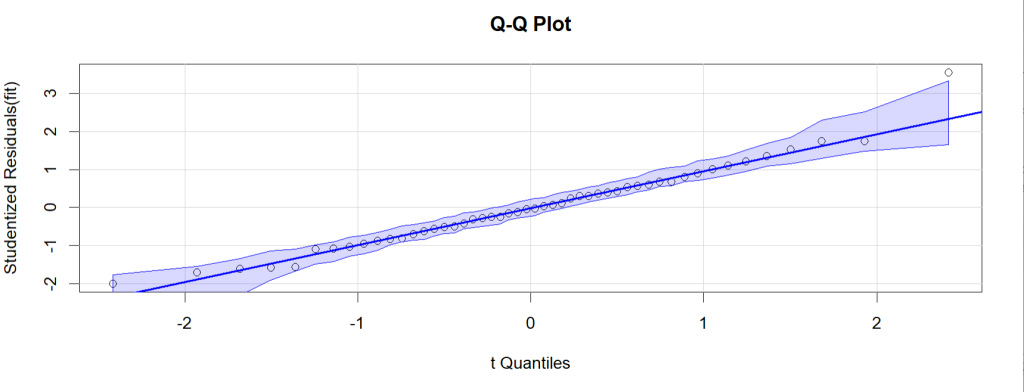
The qqPlot() plots the studentized residuals (also called studentized deleted
residuals or jackknifed residuals) against a t distribution quantiles. From the state data we can see that majority of the residuals stay very close to the straight line, and there is no missing systematic trends existing in the model. So in this example it is safe to say that the normality assumption is met.
In the next example, dependent variable mpg is regressed on variable disp, hp and wt from mtcars data frame.
#show several observations of mtcars
head(mtcars)
#output
mpg cyl disp hp drat wt qsec vs am gear
Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4
Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4
Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4
Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3
Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3
Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3
carb
Mazda RX4 4
Mazda RX4 Wag 4
Datsun 710 1
Hornet 4 Drive 1
Hornet Sportabout 2
Valiant 1
#mpg is regressed on variable disp, hp and wt from mtcars #data frame
fit <- lm(mpg ~ disp + hp + wt, data=mtcars)
#qqPlot to show residuals against theoretical quantiles
qqPlot(fit, simulate=TRUE, labels=row.names(mtcars),
id=list(method="identify"), main="Q-Q Plot")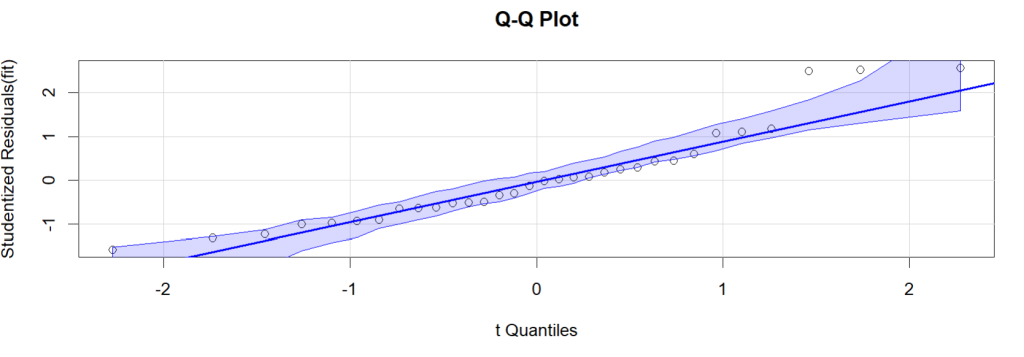
The qqPlot shows that a significant part of the residuals stay relatively far from the straight line. In addition, it seems the residuals in the middle part mostly stay under the line, while residuals in other areas over the line. So it is suspect that there are some systematic effect (e.g. second power of explanatory variables) are missed in the current regression model.
You can also watch video on learn R from our YouTube channel.
0 Comments