Calculating Type I Error and Type II Error of Hypothesis Testing using R

We provide effective and economically affordable training courses for R and Python, Click here for more details and course registration !

1. Type I and type II errors in hypothesis testing

In statistical hypothesis testing, there are usually two types of errors that the process will encounter, namely Type I and type II errors. Type I error (α) refers to the probability of rejection of a Null Hypothesis (H0) when actually it is true, and if a false Null hypothesis is missed to reject when an Alternative Hypothesis (H1) is true, then a type II error (ß) occurs.

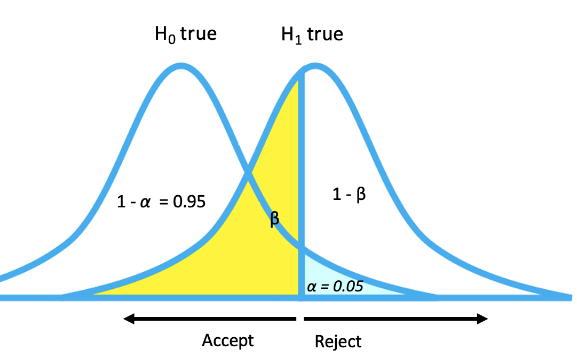
The existence of these two errors is due to the fact that H0 and H1 usually have overlap in their probability densities (see the figure below). Note that α (blue area) and ß (yellow area) behave as a trade-off when the decision critical limit (the blue vertical line) moves to the both ends, for the specified H0 and H1.

2. Calculating Type I and type II errors using R programming

We use a simple example here to illustrate calculating Type I and type II errors with R programming.

To test if a new machine acts more effectively than the current one, we form the

Null Hypothesis (H0) : p = 0.25 , and

Alternative Hypothesis (H1): p = 0.50

Then the positive cases in a sample of 20 can be modeled as a binomial distribution.

If the decision criteria is located at 8, so getting lower than or equal to 8 positive cases from 20 random samples will hold H0, and getting more than 8 positive cases in the same sample will arrive at rejection of H0 in favor of H1.

R code for solving this problem could be implemented by using function pbinom().

#probability of x occur more than 8 times among total 20
# trials, with probability 0.25 for each trial 
> type_1_error <- 1 - pbinom(8, size = 20, prob = 0.25)

> type_1_error
[1] 0.04092517

#probability of x occur less than or equal to 8 times among #total 20 trials, with probability 0.5 for each trial
> type_2_error <- pbinom(8, size = 20, prob = 0.5)
> 
> type_2_error
[1] 0.2517223

We see that when the decision rule (critical limit) is 8, the hypothesis will encounter Type I and type II errors around 0.04 and 0.25 respectively.

Now, say we have changed a little the decision rule, to move critical line to 7. Then calculate again these two errors.

#probability of x occur more than 7 times among total 20
# trials, with probability 0.25 for each trial
> type_1_error <- 1 - pbinom(7, size = 20, prob = 0.25)

> type_1_error
[1] 0.1018119


#probability of x occur less than or equal to 7 times among #total 20 trials, with probability 0.5 for each trial
> type_2_error <- pbinom(7, size = 20, prob = 0.5)
 
> type_2_error
[1] 0.131588
> 

The results show that Type I error has increased, because the decision critical line has been lowered, and the H0 will be more likely to be rejected than previous example, thus the probability of wrong rejection is enlarged. At the same time, the type II error is less than before, because less chance will happen for the missed rejection of H0 when actually H1 should be favored.

You can also watch videos on our YouTube for more vivid understanding of Type I and type II errors in Hypothesis testing.