Estimating simple linear regression model using lm() in R

We provide effective and economically affordable training courses for R and Python, Click here for more details and course registration !

Linear regression is widely used to model the relationship between response or dependent variable and explanatory or independent variables. The parameter in the model has linear form. When there is only one explanatory assumed in the model, it is called simple linear regression.

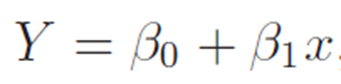
In R programming, lm() function maybe the most widely used function to estimate a linear regression model. The basic form of the function is :

m_fit <- lm(formula, df)

Where

df is the data frame where variables come from,

formula shows the response and explanatory variables, using plus symbol to separate explanatory variables. The following code shows a simple linear regression estimation between response variable ‘weight’ and explanatory variable ‘height’ from data set ‘women’ from R base installation. The result of lm() function is assigned to a list object m_fit.

m_fit <- lm(weight ~ height, data=women)

After the model is estimated, we can show the estimation result using summary() function.

> summary(m_fit)

#result
Call:
lm(formula = weight ~ height, data = women)

Residuals:
    Min      1Q  Median      3Q     Max 
-1.7333 -1.1333 -0.3833  0.7417  3.1167 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -87.51667    5.93694  -14.74 1.71e-09 ***
height        3.45000    0.09114   37.85 1.09e-14 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1.525 on 13 degrees of freedom
Multiple R-squared:  0.991,	Adjusted R-squared:  0.9903 
F-statistic:  1433 on 1 and 13 DF,  p-value: 1.091e-14

The information in summary() function includes the coefficient estimates, residuals, and R-squared value. Residuals are the difference between observed response variable and fitted value from the linear model. In the coefficients part, in addition to the point estimate of two coefficients (intercept – beta0, height – beta1), the standard errors as well as the corresponding t-statistics and p-values are also listed. Both coefficients are significant because the p-values are fairly close to zero.

In the last part of the result in summary() function, there are R-squared value. The two values are both close to 0.99, which state that almost 99% of the variation in the response variable is explained by the explanatory variable. In a simple linear regression model, this value also equals to the square of correlation coefficient between these two variables. Alternatively, the result shows F-statistics and corresponding p-value. An almost zero p-value also says the model has significant power to explain the response variable numerically by using the explanatory variables.

You can also watch the video on R programming training from our YouTube channel here.