Binomial distribution is a discrete random distribution modeling the probability of event success number x in N Bernoulli trial. A Bernoulli trial is an experiment of binary (success/fail) result with a constant success rate in each trial. To calculate the probability for individual success number x in R, function dbinom() can be used. In the following example, the probabilities for integer 0 to 10 in a N=10 Bernoulli trial with success rate 0.2 are calculated and plotted.
#probabilities of success numbers, between o and 10
#of a Binomial distribution, with success rate 0.2
probabilities <- dbinom(x = c(0:10), size = 10, prob = 0.2)
probabilities
#output
[1] 0.1073741824 0.2684354560 0.3019898880 0.2013265920 0.0880803840
[6] 0.0264241152 0.0055050240 0.0007864320 0.0000737280 0.0000040960
[11] 0.0000001024
plot(0:10, probabilities, type = "l")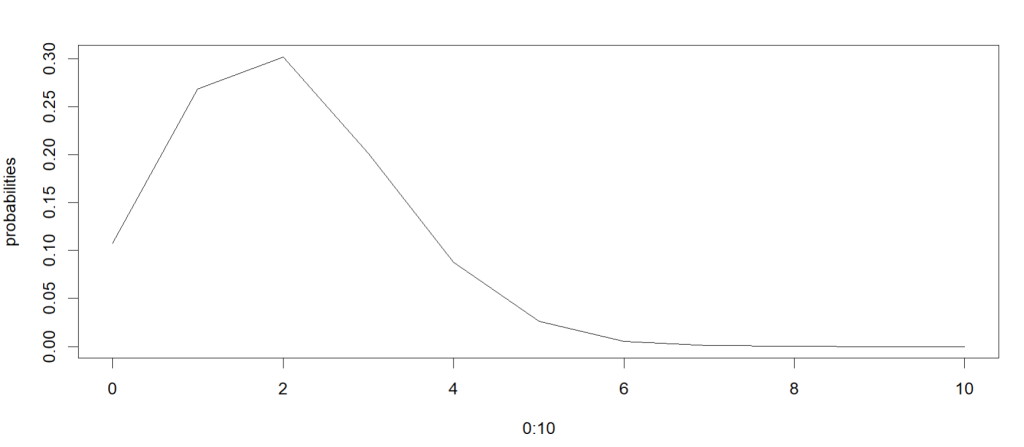
If we want to know the cumulative probabilities up to a certain value in a Binomial distribution, we can use pbinom() in R. The following example shows the cumulative probabilities of success numbers equal to or less than 3 in a Binomial distribution of size N, and success rate 0.2.
pbinom(3, size = 10, prob = 0.2)
#output
[1] 0.8791261
0 Comments