Poisson distribution is used to model the random number (x) of event occurrence during a Poisson process, which focus on the occurrence of same random events during a fixed time period (t) with a constant occurring rate (lambda). The calculation formula of the probability x can be expressed as:
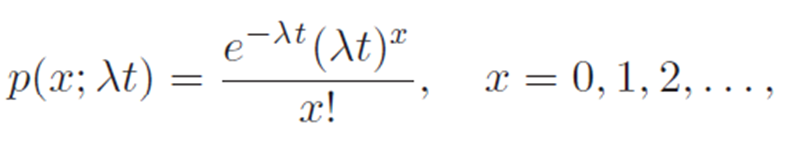
In R programming, function dpois() can be applied to compute Poisson probabilities. Next code example shows how to calculate Poisson probabilities for events occurrence between 1 and 15 in a Poisson process with lambda * t = 10.
#a vector for different events occurrence between 1 and 15
pnum <- seq(1:15)
#probabilities of events occurrence in a Poisson process with lamba * t = 10
ppoi <- dpois(pnum,10)
ppoi
#output
[1] 0.0004539993 0.0022699965 0.0075666550 0.0189166374 0.0378332748
[6] 0.0630554580 0.0900792257 0.1125990321 0.1251100357 0.1251100357
[11] 0.1137363961 0.0947803301 0.0729079462 0.0520771044 0.0347180696
#plot the probabilities
plot(ppoi)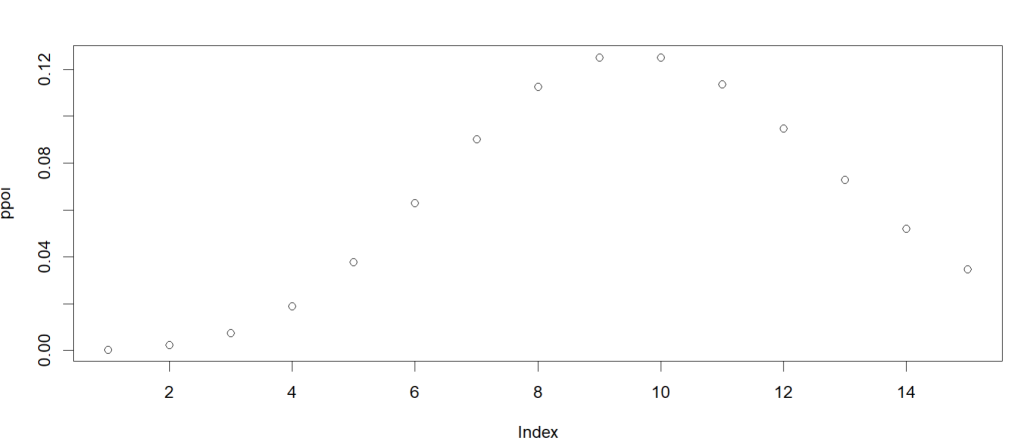
We can see the highest probability exists around 10, which is the mean of the distribution here.
0 Comments