We provide effective and economically affordable training courses for R and Python, Click here for more details and course registration !
Beta distribution is a family of distributions which are used to model the probability of continuous random variables defined on [0, 1]. There are two parameters , α and β in Beta distribution. A continuous uniform distribution defined on [0, 1] is actually a special case of a beta distribution, when both α and β equal 1. Beta distribution is a important prior distribution in Bayesian statistics, due to its fact that beta distribution is the conjugate prior for many other statistical distributions, such as Bernoulli, binomial distribution, just name a few. This why beta probability is often called ‘The probability of probability’.
- Probability density function of a beta distribution
The continuous random variable X has a beta distribution with parameters
α > 0 and β > 0 if its density function is given by
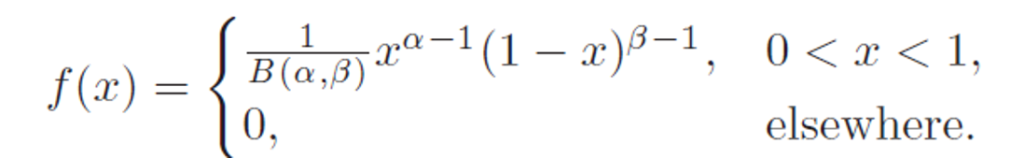
Where
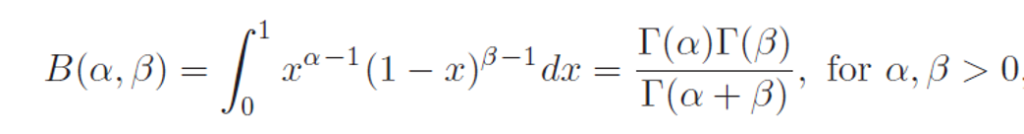
And
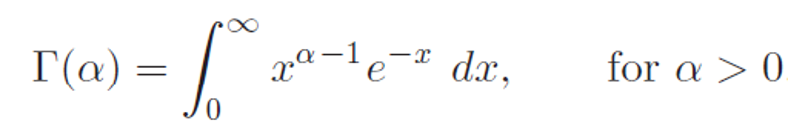
2. Using Beta distributions in R
In R programming, probability functions take the form [dpqr]distribution_abbreviation()
Where
d = Density or probability
p = Cumulative Distribution function
q = Quantile function
r = Random number generation
And for beta distribution, there are normally four following functions that are often used.
dbeta()
pbeta()
qbeta()
rbeta()
Example 1: Calculate a uniform distribution on [0, 1] using dbeta()
# Creating a vector X
x = seq(0, 1, by = 0.05)
# Plotting the beta density in terms of each value in X
plot(x, dbeta(x, 1,1), xlab="X",
ylab = "Uniform distribution", type = "l",
col = "Red")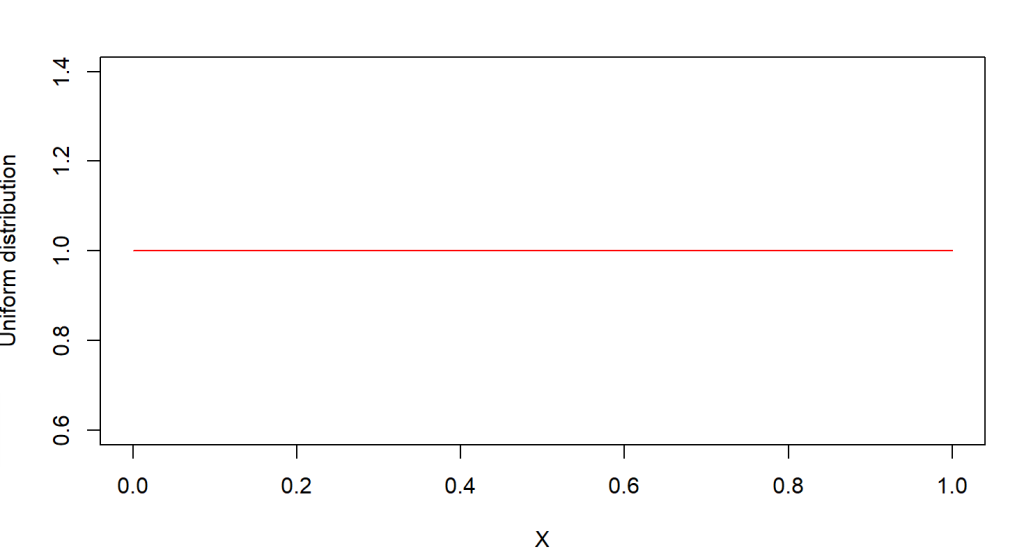
Example 2: Calculating a beta density with 5, 8 for α and β using dbeta()
# Creating the vector X on [0, 1]
x = seq(0,1, by=0.1)
# plot the relationship between density and x
plot(x, dbeta(x, 5,8), xlab = "X",
ylab = "Beta Density with parameter 5, 8", type = "l",
col = "Red")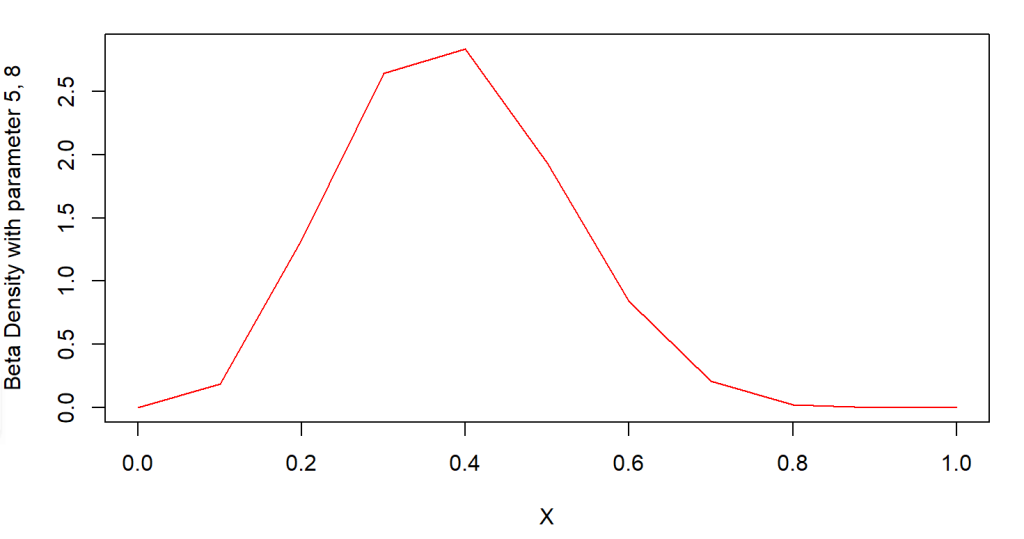
Example 3: Calculating cumulative probabilities using pbeta()
# create a data frame
df <- data.frame(
dvec <- c(seq(0, 1, by = 0.01)),
stringsAsFactors = FALSE
)
# calculate and plot beta cumulative probabilities
# for a variable vector in dataframe
cump <- pbeta(df$dvec, shape1 = 5, shape2 = 8)
par(mar = rep(2,4))
plot(cump)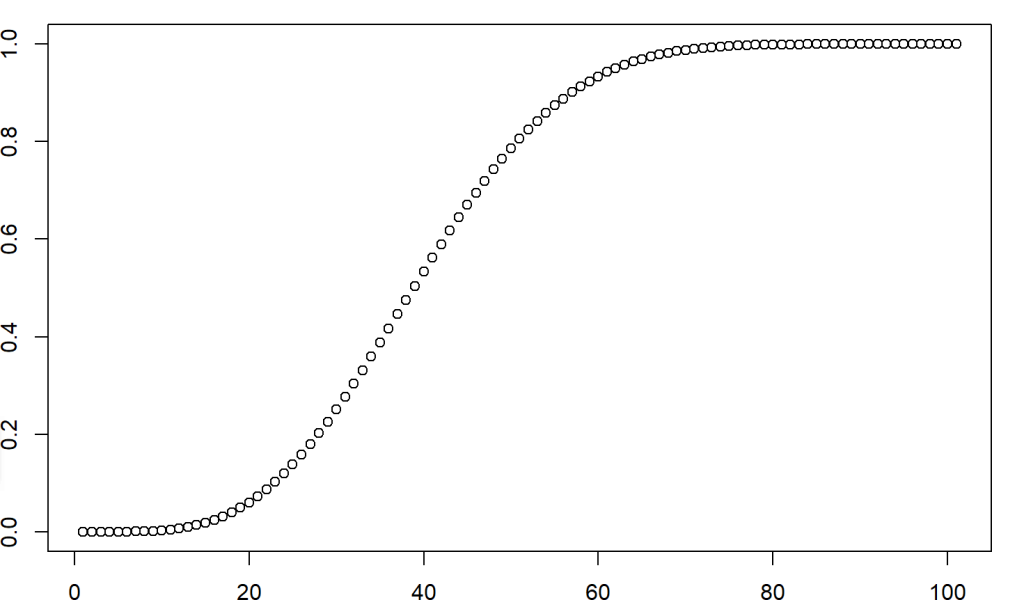
Example 4: Calculating beta distribution quantile values using qbeta()
#create a vector of cumulative probabilities
p_vec <- c(seq(0, 1, by = 0.001))
#calculating quantile values with respect to cumulative
# probability values
q_vec <- qbeta(p_vec, shape1 = 5, shape2 = 8)
par(mar = rep(2,4))
plot(q_vec)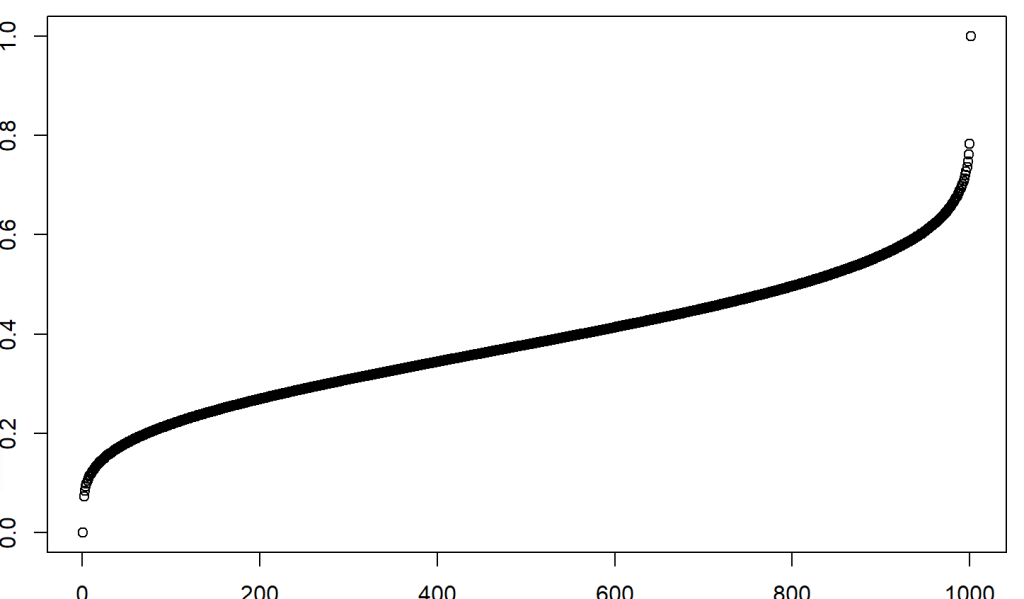
Example 5: Generating random variates from a beta distribution using rbeta()
r_vec <- rbeta(50, shape1 = 5, shape2 = 8)
r_vec
> r_vec
[1] 0.42673754 0.66754889 0.34116474 0.39604894 0.47921165 0.60826630
[7] 0.46580700 0.20054064 0.16736570 0.40624758 0.19898141 0.30119454
[13] 0.21065760 0.25934088 0.47224206 0.34144223 0.69418006 0.50641507
[19] 0.38900934 0.25232249 0.35749355 0.22484752 0.19716958 0.31350510
[25] 0.22997062 0.49352156 0.30149413 0.44157550 0.47368579 0.26791433
[31] 0.40460251 0.08595809 0.03383054 0.45230428 0.21502300 0.47839476
[37] 0.68103231 0.52249427 0.37370569 0.40081123 0.56911762 0.43524239
[43] 0.20376494 0.41787705 0.47686581 0.28331784 0.51510437 0.26042955
[49] 0.42863551 0.43587389
>
0 Comments