We provide effective and economically affordable training courses for R and Python, Click here for more details and course registration !
The exponential distribution is modeling the probability distribution of the random time until next event occur in a Poisson event process. A Poisson event process has a constant occurring rate during an interval. Exponential distribution is a particular case of the gamma distribution when the shape parameter (alpha) equals 1.
Exponential distribution has the following probability density function.
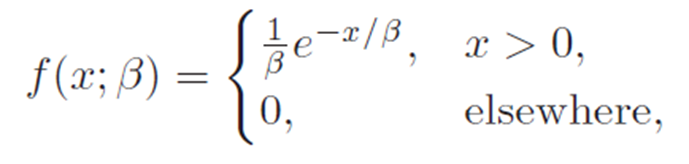
The mean of an exponential distribution equals to beta.
Generally, exponential distributions can be implemented using expon() model from scipy.stats() module. Following code shows several examples for random number generation, calculating probability densities, and calculating cumulative probabilities for exponential distributions in Python.
Example 1: Generating random numbers from an exponential distribution.
from scipy.stats import expon
import numpy as np
import matplotlib.pyplot as plt
#scale or beta, is the average time between two events
# it is the reciprocal of hazard rate lambda in poisson distribution.
# Random 10 Variates from exponential distribution with beta # = 2
R = expon.rvs(scale = 2, size = 10)
print ("Random Variates : \n", R)
#output
Random Variates :
[0.23565008 0.39198579 3.78138116 4.38514265 4.05855378 0.61639563
3.65629436 1.49444996 6.99201959 3.47163068]Example 2: Calculating probability densities from an exponential distribution.
from scipy.stats import expon
import numpy as np
import matplotlib.pyplot as plt
#a numpy array for random variables
quantile = np.arange (0.01, 3, 0.1)
#probability densities for the array, from exponential
#distribution with beta = 1
Den_city = expon.pdf(quantile, scale = 1)
plt.plot(quantile, Den_city)
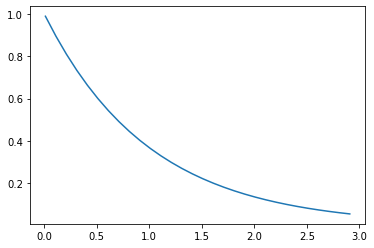
Example 3. Calculating cumulative probabilities for random variates from exponential distributions.
from scipy.stats import expon
import numpy as np
import matplotlib.pyplot as plt
#cumulative probability
quantile = np.arange (0.01, 9, 0.1)
Cum_prob = expon.cdf(quantile, scale = 1)
plt.plot(quantile, Cum_prob)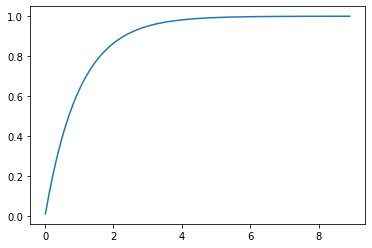
Example 4. To calculate the probability that the time until next event coming larger than 3 minutes, when the average time until next event coming is 2 minutes, from an exponential distribution.
from scipy.stats import expon
import numpy as np
import matplotlib.pyplot as plt
scale = 2
p_large_3 = 1 - expon.cdf(3, scale = 2)
p_large_3
#result
Out[18]: 0.2231301601484298
You can also watch our Python course full video from our YouTube channel.
0 Comments