Using Lognormal distributions in R programming

We provide effective and economically affordable training courses for R and Python, Click here for more details and course registration !

1. Introduction of Lognormal distribution

Lognormal distribution in probability and statistics is used to model the distribution of a positive random variable Y, if Y = ln(X) has a normal distribution with mean μ and standard deviation σ.

The probability density function for a Lognormal variate is somewhat similar as a Normal distributed variable:

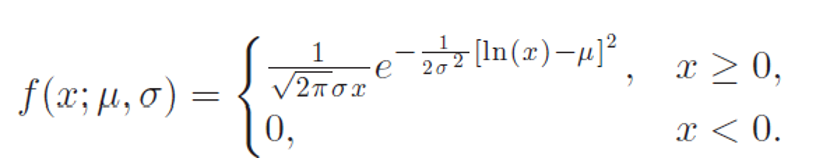
And the mean and variance for variable from Lognormal distribution are (note μ and σ on the right side come from the density function):

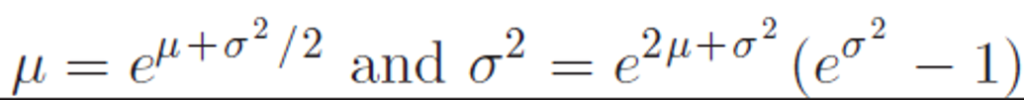
2. Using R functions to calculate Lognormal distributions.

We can use dlnorm() function to calculate the probability density of Lognormal variates. The basic form of the function is dlnorm(X, μ=0, σ=1).

For example, the following code shows the calculation of probability density for a Lognormal distributed variable vectors between 1 and 100, with μ=5, σ=2 in the density function.

> x <- seq(1, 100, by = 0.1)
> y <- dlnorm(x, 5,2)

> # Plot a graph
> plot(x, y)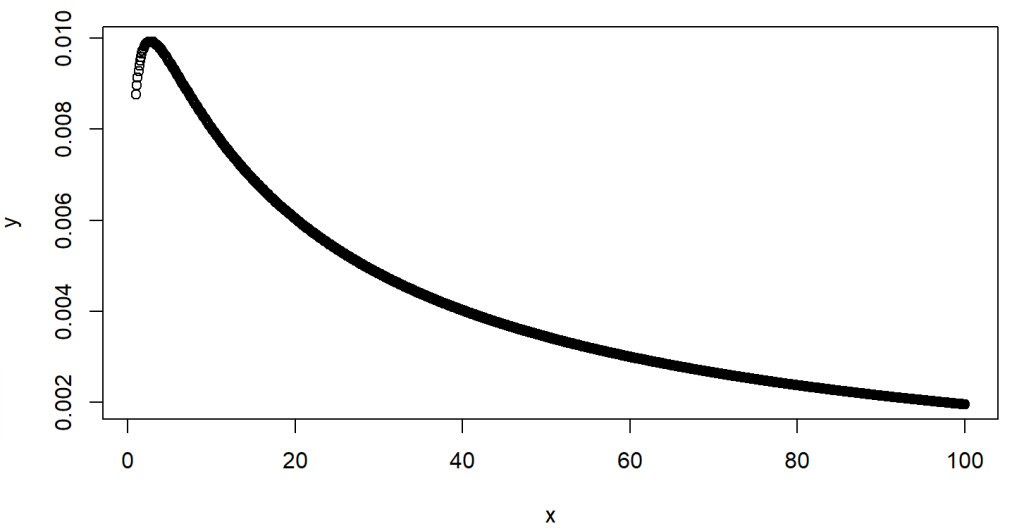

plnorm() function is used to compute the cumulative probabilities for Lognormal variates. The basic form of the function is plnorm(X, μ=0, σ=1). The following code illustrate the calculation of cumulative probabilities for a Lognormal distributed variable vectors between 1 and 100, with μ=5, σ=2 in the density function.

# create a vector of random variables
> x <- seq(1, 100, by = 0.1)
#calculate probabilities of those random variables
#from a lognormal distribution with μ=5,  σ=2 in density #function.
> y <- plnorm(x,5,2)
> plot(x,y)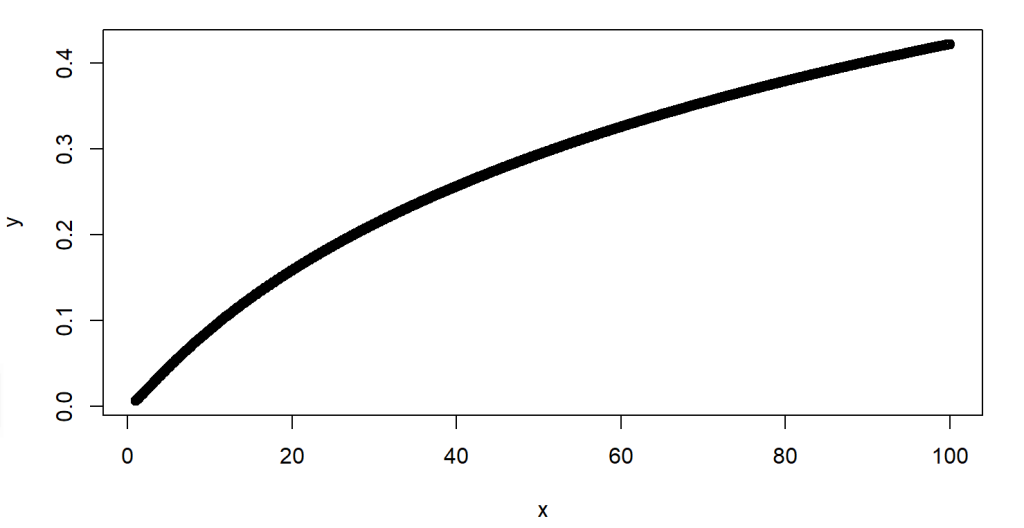

From the foregoing figure, wen can simply find that about 1/4 of the values are below 25 in this distribution.

qlnorm() function can be seen as an opposite operation of plnorm(). The aim of the function is to find the quantile or random number values associated with the known cumulative probabilities. The following code shows how to get quantile values from a Lognormal distribution , with a probability vectors between 0 and 1,

# Creating a vector between 0 and 1, denoting the known #cumulative probabilities
> probs <- seq(0, 1, by = 0.05)
> calculating quantile values from a lognormal distribution #with μ=5,  σ=2 in density function.
> x <- qlnorm(probs, 5, 2)
> plot(probs,x)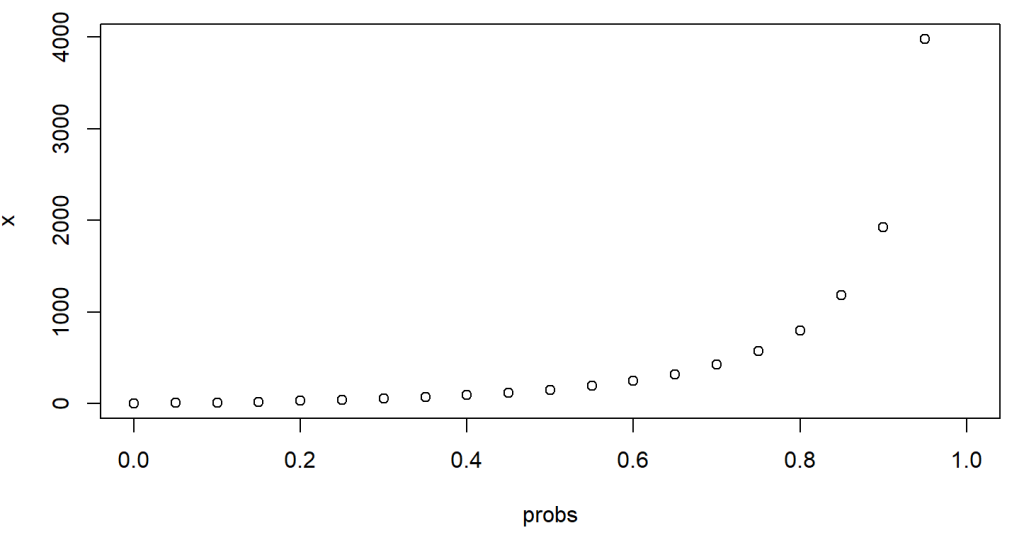

From the figure, we can simply get the value about 2000 associated with cumulative probability around 0.9. It says about 90% of the random numbers from this Lognormal distribution have values lower than 2000.

To draw random numbers from a given Lognormal distribution with known parameters μ and σ in density function, you can simply use rlnorm() function.

The following code is used to draw 10000 such random numbers from a Lognormal distribution with μ=0, σ=1 in density function.

> N <- 10000

# generate 10000 random numbers from a Lognormal distribution #with μ=0,  σ=1 in density function.
> x <- rlnorm(N)
> mean(x)
[1] 1.67055
#use formula to calculate mean
> sqrt(2.718) 
[1] 1.648636
> 

For a video illustration of this and more posts, you can visit our YouTube here.