Using t-distribution and t-test with R

We provide effective and economically affordable training courses for R and Python, Click here for more details and course registration !

1. Introduction of t-distribution and t-test

A Student t-distributed random variable is modeling the ratio between a standard Normal random variate and square root of a Chi-squared random variable divided by its degrees of freedom.

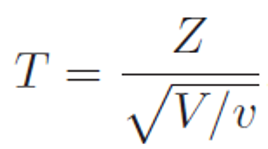
Where

Z is a random variable that follows standard Normal distribution,

and V is a random variable that follows a Chi-squared distribution with degrees of freedom v.

The probability density function for t-distribution is given as

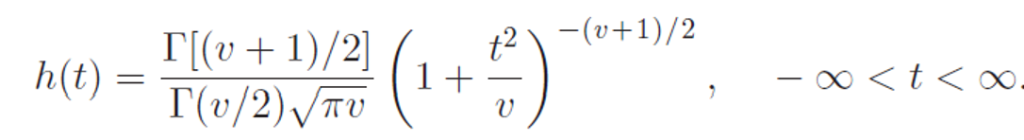
Where

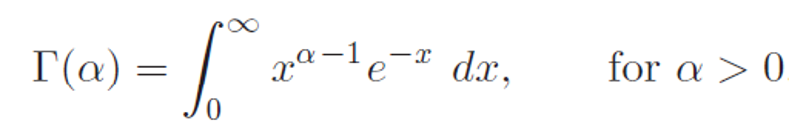
denotes a gamma function.

t-distribution is often used to test a population mean under a Null hypothesis (H0) : μ = μ0 , against an Alternative hypothesis (H1): μ not equal to μ0, with random samples in small size (e.g. < 30) from an approximately normally distributed population.

Let X1,X2, . . . , Xn be n independent random numbers coming from a normal population with mean μ and standard deviation σ. Let sample average and sample variance computed as following

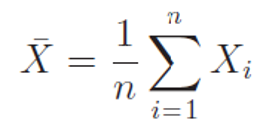
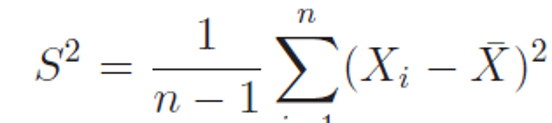
then the test statistics

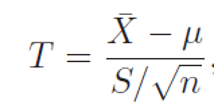
follows a t-distribution with v = n − 1 degrees of freedom. If the T is located at in the critical region, then the test will come to a conclusion of rejecting H0 in favor of H1, or say the test is significant at level α.

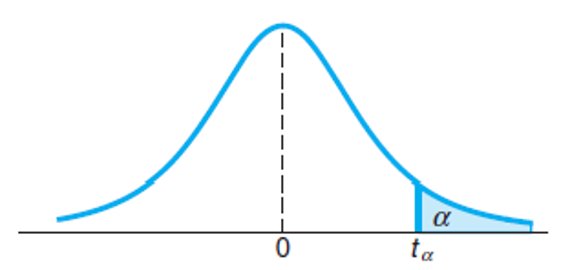
2. Using t-distribution with R

In R programming, there are several functions dealing with t-distribution:

dt(): Probability density
pt(): Cumulative probability
qt(): Quantile value
rt(): Random number generation

dt() function is used to find the value of probability density (pdf) of a random variable x from t-distribution. The basic form of the function is

dt(x, df)

where x is usually a vector represents a series of random variables, and df is the degrees of freedom. Following code example shows how to calculate and plot probability densities for random variables between 0 and 5 from a t-distribution with degrees of freedom 7.

#create a vector between 0 and 5
x_vec <- seq(0, 5, by = 0.1)
df <- 7

#dt() calculating probability density
plot(x_vec, dt(x_vec,df))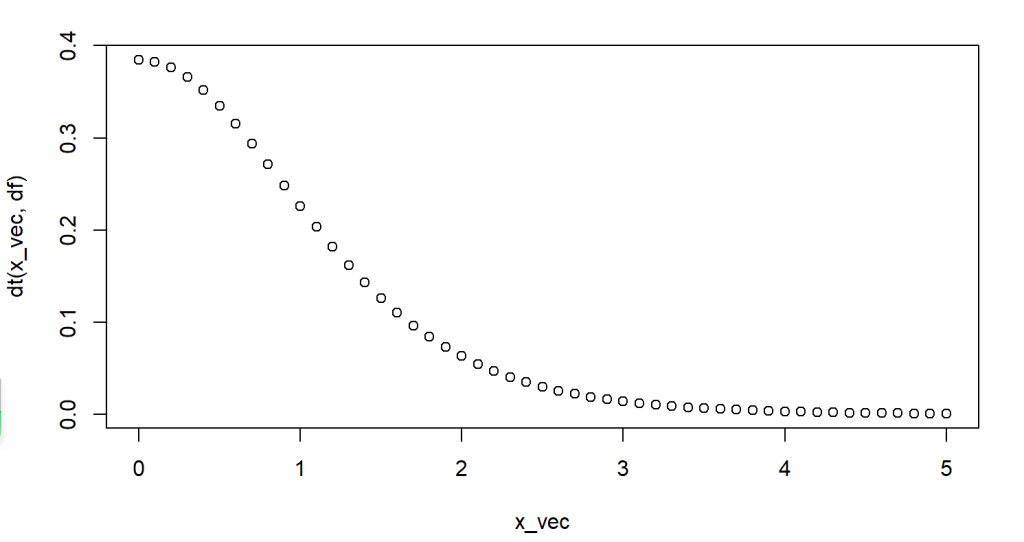

pt() function is used to calculate the cumulative probability (CDF) till a given value following t-distribution. The basic form of the function is

pt(q, df)

where

q represents variates from t-distribution, and df denotes degrees of freedom.

The following code example show calculating and plotting cumulative probabilities for variates between 0 and 5, which follow a t-distribution with degrees of freedom 7. And from the figure we can see that about 80% of the values are less than or equal to 1 in this distribution.

#create a vector of random variables
x_vec <- seq(0, 5, by = 0.1)
df <- 7

#pt() function for calculating cumulative probabilities
#from t-distribution 
plot(x_vec, pt(x_vec,df))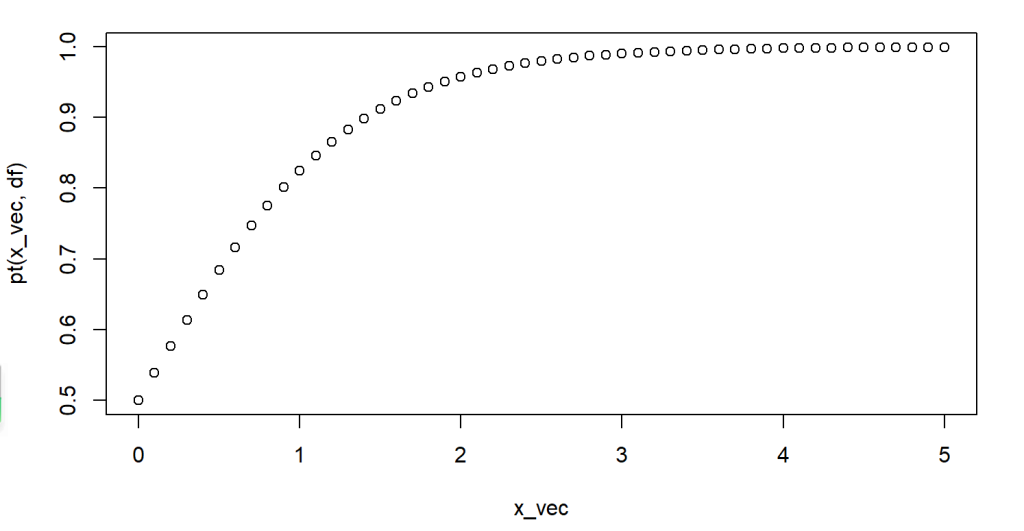

function qt() is the opposite operation of pt(), and is used to calculate the t-distribution quantile value, from the given cumulative probability. The basic form of the function is

qt(p, df)

where p represents the cumulative probability, and df is for degrees of freedom.

The following code example shows calculating and plotting the quantile values for the given cumulative probabilities between 0 and 1, for a t-distribution of degrees of freedom 7. From the figure we can also see that about 80% of the values in the given distribution have values below 1.

#create a vector representing cumulative probabilities
probs <- seq(0, 1, by = 0.05)
df <- 7

#qt() for calculating t-distribution quantile values
plot(probs, qt(probs,df))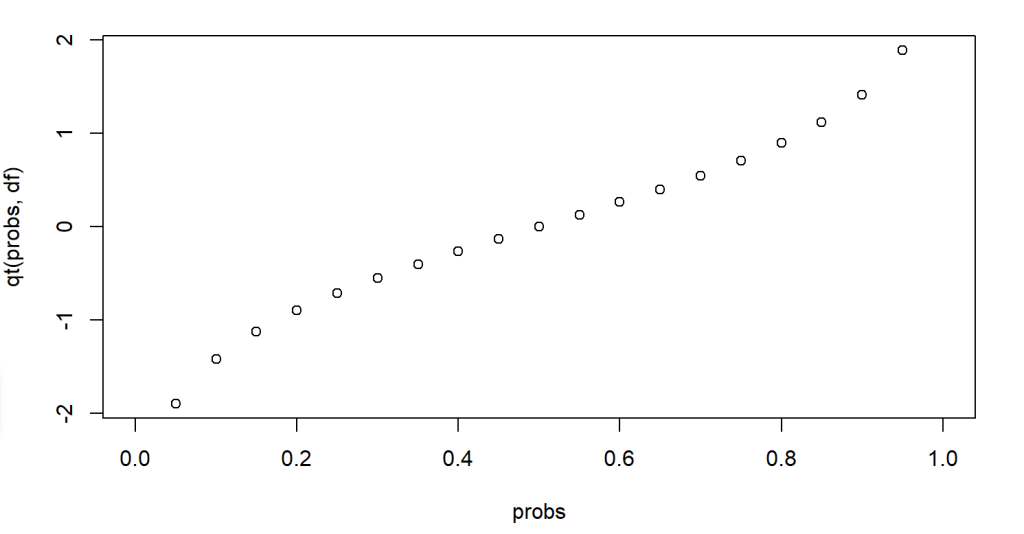

rt() is used to generate random variates from a given t-distribution. The basic syntax of the function is

rt(N, df)

where N is the number of values to generate, and df represents degrees of freedom.

Following code example show generating 10000 random values from a t-distribution of degrees of freedom 10.

# set how many values to generate
N <- 10000
df <- 10

#rt() for t-distribution variates generation 
plot(hist(rt(N,df)))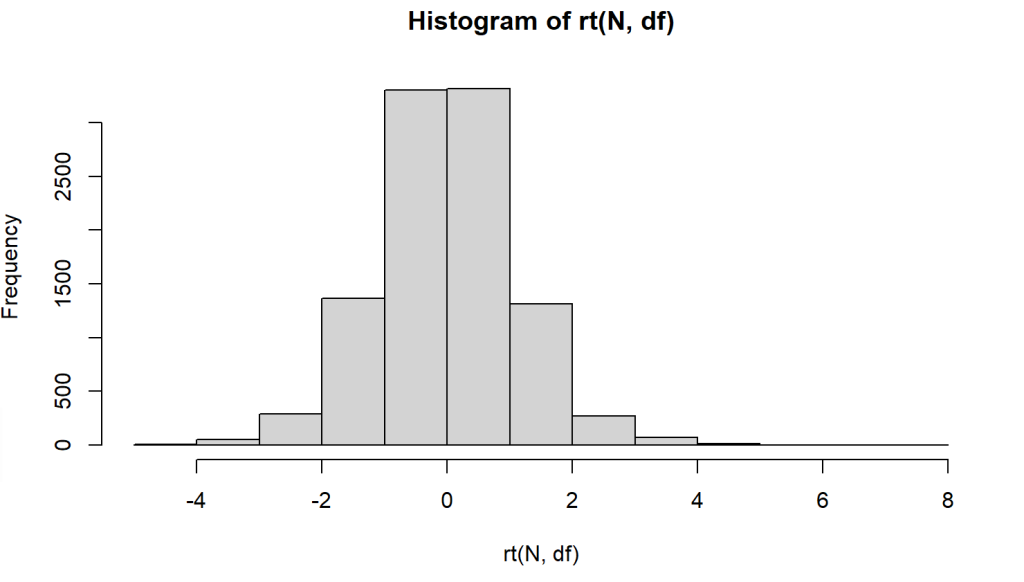

3. Using t-test with R

The following example shows how to use t-distribution functions for t-test in R.

Description of the example:

A medical researcher claims that the population mean yield of a certain medical product is 500 cm. To check this claim he samples 25 batches per week. If the computed t-value falls between −t0.05 and t0.05, he will hold the claim. What conclusion should he draw from a sample that has a mean X-Ba = 518 cm and a sample standard deviation s = 40 cm ? Assume the distribution of the population to be approximately normal.

Solution:

# first we calculate the critical value of t0.05 
# using qt(probs, df)
t_cri <- qt( 1-0.05, 24)
t_cri   
[1] 1.710882

# then we calculate the sample t test statistics
t_sample <- (518 - 500) / (40/sqrt(25))
t_sample    
[1] 2.25

#we can also calcualte the p_value assocated with t_sample
p_sample <- 1 - pt(t_sample, 24)
p_sample   
[1] 0.01694426

As t_sample > t_cri, it also shows p_sample < 0.05, the medical researcher is likely to reject the claim and conclude that the process yields is probably larger than 500 cm.

You can also watch full video on R tutorial from our YouTube channel.