We provide effective and economically affordable training courses for R and Python, Click here for more details and course registration !
- Introduction of Weibull distribution
Weibull distribution, named after Swedish mathematician Waloddi Weibull, is a continuous distribution which is widely used to model the distribution of random time between events. Exponential distribution, which is used to model the random time until next event occurs and have so-called memoryless feature or constant failure rate. In order to relax this memoryless condition, analysts may use either Gamma distribution or Weibull distribution instead.
Weibull distribution has two following parameters:
k – shape parameter , and
lambda – scale parameter.
The following figure shows several probability density functions of Weibull distribution, in terms of different parameters.
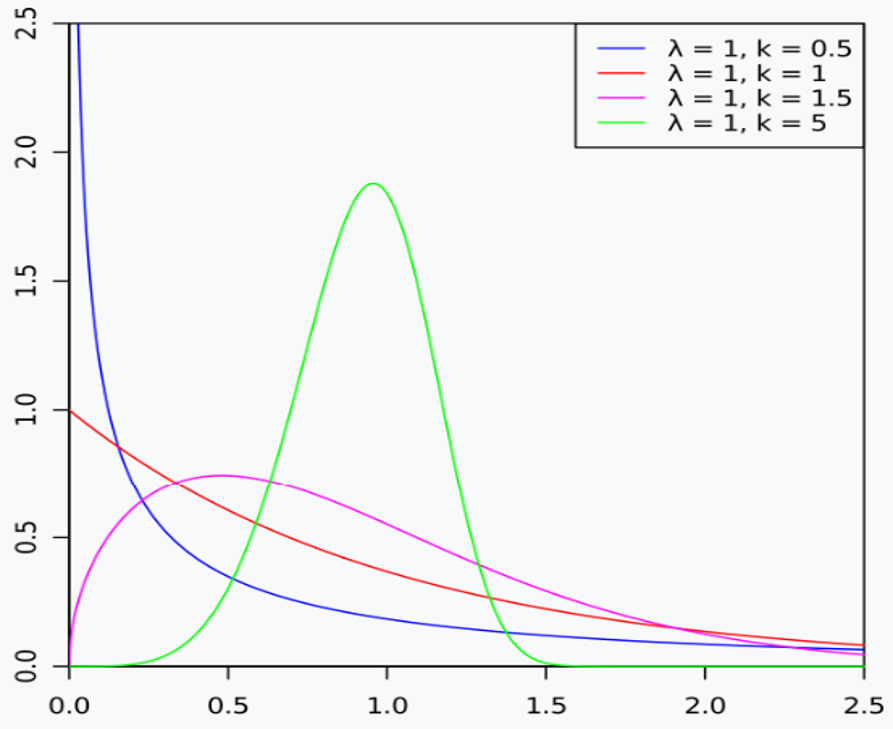
Weibull distribution has the following probability function:
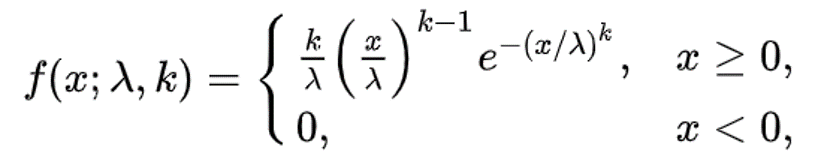
Exponential distribution is actually one kind of Weibull distribution, when K = 1.
2. R functions for calculating Weibull distribution
There are primarily four functions in R programming that can be used for Weibull distribution calculation :
dweibull() – Probability density
pweibull() – Cumulative probability
qweibull() – Quantile value
rweibull() – Random number generation
dweibull() is used to compute probability densities for random variables from a given Weibull distribution. The basic form of the function is dweibull(x, shape, scale),
Where
x is a vector of Weibull variables, and shape and scale parameters both have default value 1.
The following code example illustrates the computation and plot of probability densities for Weibull variates between 0 and 10, with shape and scale both located at 1.
# Creating a sequence of x-values
> x <- seq(0, 10, by = 0.2)
> k<- 1
> lambda <- 1
# Calling dweibull() Function, to compute probability #densities
> y <- dweibull(x, shape = k, scale=lambda)
#plot densities
> plot(x, y)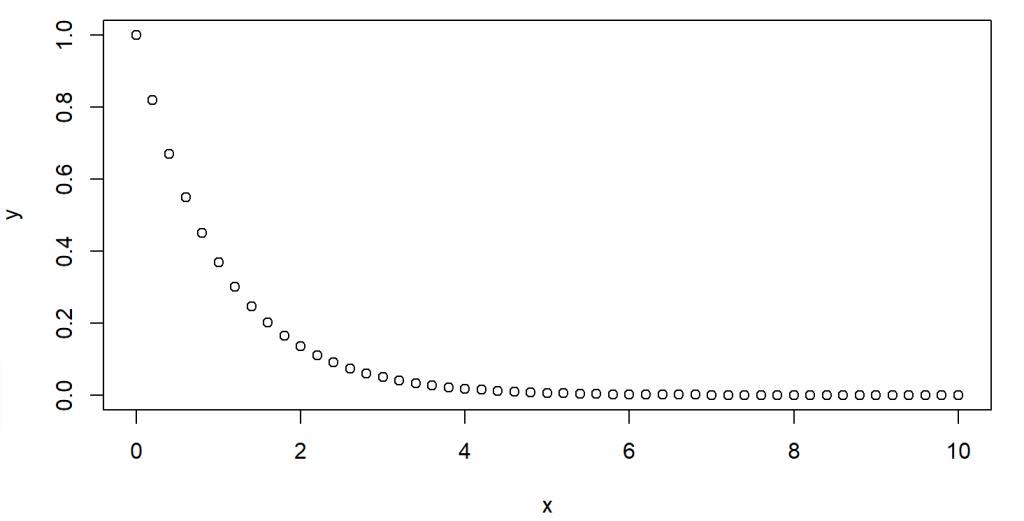
pweibull() function is used to compute the cumulative probability for a range of random variables from Weibull distribution. The basic form of the function is pweibull(x , shape, scale),
Where
x is a vector of Weibull variables, and shape and scale parameters both have default value 1.
Following example shows the calculation of cumulative probabilities for a Weibull variates between 0 and 10, with shape and scale parameters located at 2 and 5, respectively.
# Creating a vector of Weibull variates
> x <- seq(0, 10, by = 0.2)
> k<- 2
> lambda <- 5
>
# Calling pweibull() Function to calculate cumulative #probabilities
> y <- pweibull(x, shape = k, scale=lambda)
> plot(x, y)
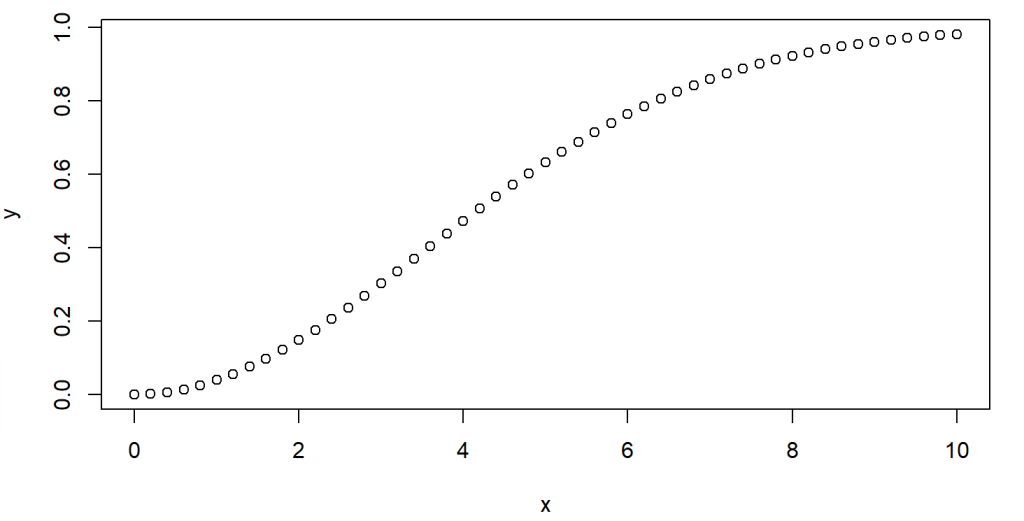
From the curve, we can see that around 50% of the variables of this distribution are less than or equal to 4.
qweibull() function is the opposite operation of pweibull(). It is used to compute the quantile values of a Weibull distribution, in terms of the given cumulative probabilities. The basic form of the function is qweibull(prob, shape, scale),
Where
prob represents the vector of cumulative probabilities, and shape and scale parameters both have default value 1.
The following code example presents the calculation of quantile values from a Weibull distribution whose shape and scale parameters both equal to 3, given the known cumulative probabilities between 0 and 1.
#vector of cumulative probabilities
probs <- seq(0, 1, by = 0.1)
> k<- 3
> lambda <- 3
# Calling qweibull() Function, to compute quantile values
> y <- qweibull(probs, shape = k, scale=lambda)
> plot(probs, y)
> 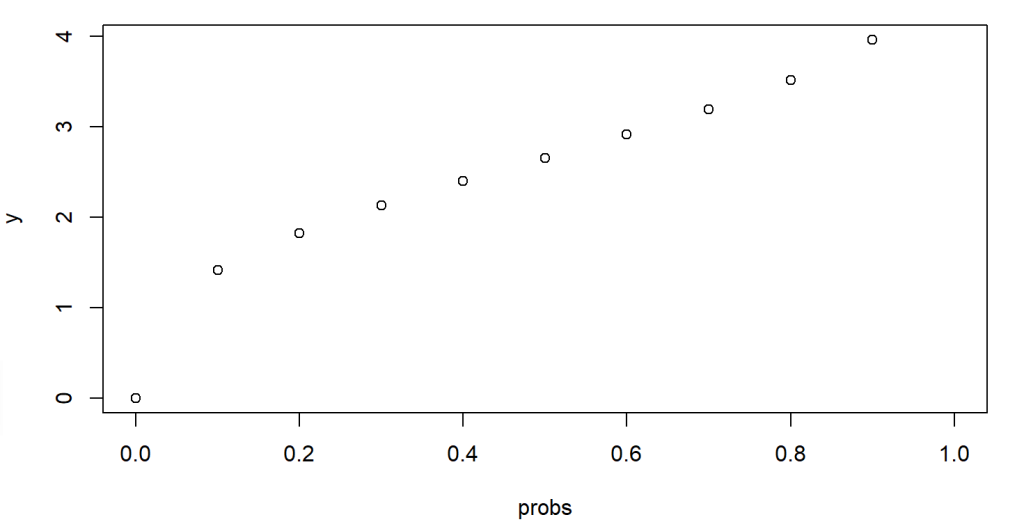
The figure shows that about 40% of the variables in this distribution have values lower than 2.5 .
rweibull() is used to generate random variables from a given Weibull distribution. The basic form of the function is rweibull(N, shape, scale),
Where
N denotes the number of random values to be generated,
and shape and scale both have default value 1.
The following code example shows the generation and plot of 10000 random values from a Weibull distribution with both shape and scale located at 3.
N <- 10000
> k<- 3
> lambda <- 3
# Calling rweibull() Function to generate random values from #a given Weibull distribution
> x <- rweibull(N, shape = k, scale=lambda)
#first 10 values
>x[1:10]
[1] 2.732754 1.859545 2.897181 3.059580 4.030458 3.764852 1.305473
[8] 1.180479 1.372219 2.271262
> plot(hist(x))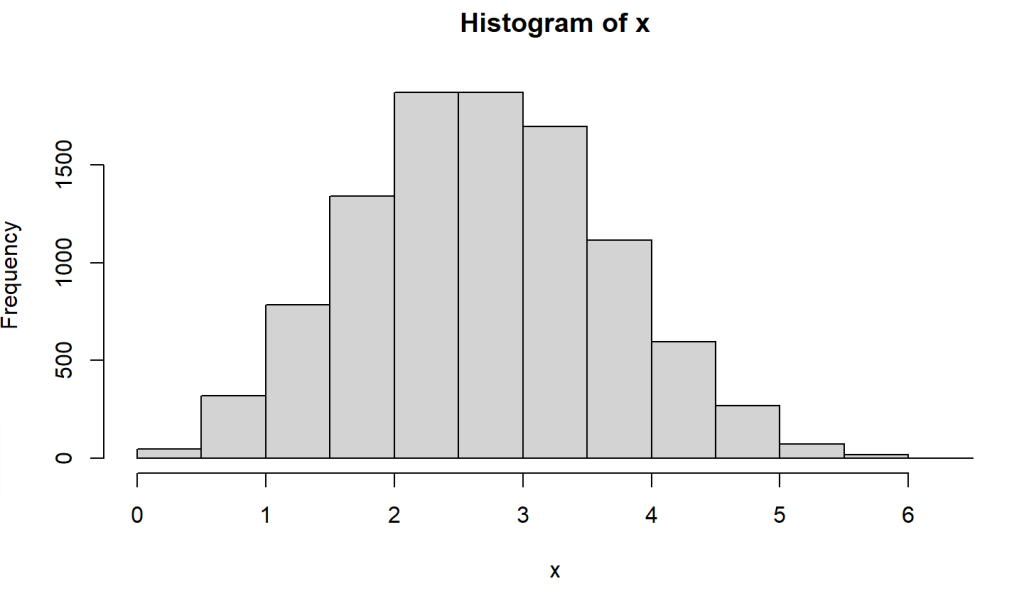
You can also visit our YouTube channel about using Weibull distribution in R.
0 Comments