Working with normal distributions in Python

We provide effective and economically affordable training courses for R and Python, Click here for more details and course registration !

Normal distribution is describing random variables with bell-shaped probability density functions. Normal distribution is widely used in data science because large sample random variates have a mean value which follows approximate normal distribution if variates are independently drawn from any distributions. The probability density function for normal distribution is determined by two parameters: mean(miu) and standard deviation(sigma).

Next, we show using normal distribution in Python programming.

First, we draw a histogram which represent thousands of random numbers drawn from a normal distribution.

#Histogram plotting Normal Distribution

#import numpy and matplotlib module
import numpy as np
import matplotlib.pyplot as plt
  
# Mean of the distribution
Mean = 32
 
# satndard deviation of the distribution
Standard_deviation  = 8
  
# sample size
size = 3200
  
# creating a normal distribution data array
values = np.random.normal(Mean, Standard_deviation, size)
  
# plotting histogram of this array
plt.hist(values, 10)
# plotting mean line
plt.axvline(values.mean(), color='k', linestyle='dashed', linewidth=2)
plt.show()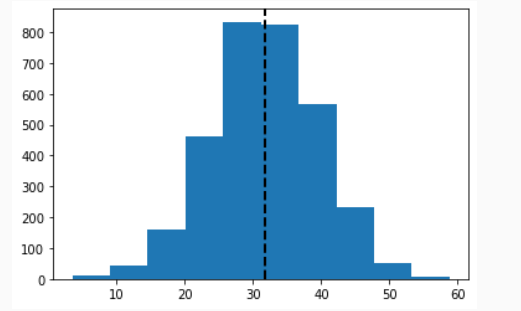

Next example is using normal distribution functions in Python to calculate the probabilities associated with a sample of student testing scores.

Suppose student test scores follow Normal probability distribution with mean 81 and standard deviation 18.

Question 1: Calculate the percentage of students who have scores less than 60.

Question 2: How much percentage of students having scored better than 95 in testing?

Question 3: Which testing score under which there are about 80% of all the students ?

Following code examples show how to implement normal distribution to solve these problems in Python.

#Solution to question 1
# import required libraries: norm function from scipy.stats 
#module, and numpy module
from scipy.stats import norm
import numpy as np
 
# Given normal distribution information 
mean = 81
std_dev = 18
total_students = 100
score = 60
 
# Calculate z-score, the standardized value for 60
z_score = (score - mean) / std_dev
 
# Calculate the probability of getting a score less than 60
#using norm.cdf() function
#cdf() function is used to calculate the cumulative #probability for all the random values less than or equal to
#a value
prob = norm.cdf(z_score)
 
# Calculate the percentage of students who got less than 60 marks
percent = prob * 100

# Print the result
print("Percentage of students who are worse than 60 in marks:", round(percent, 2), "%")

#Result
Percentage of students who are worse than 60 in marks: 12.17 %

#Solution to question 2
# import required libraries, norm module from scipy.stats
#module , and numpy module
from scipy.stats import norm
import numpy as np
 
# Given distribution information
mean = 81
std_dev = 18
total_students = 100
score = 95
 
# Calculate z-score , the standardized score for 95
z_score = (score - mean) / std_dev
 
# Calculate the probability of getting a less than 95
#using norm.cdf() function
prob = norm.cdf(z_score)
 
# Calculate the percentage of students who got more than 95 #marks
percent = (1-prob) * 100
# Print the result
print("Percentage of students who have better than 95 marks: ", round(percent, 2), " %")

#Result
Percentage of students who have better than 95 marks:  21.84  %

#Solution to question 3
# import required libraries, norm module from scipy.stats
#module , and numpy module
from scipy.stats import norm
import numpy as np
 
# Given statistical information
mean = 81
std_dev = 18
total_students = 100
q_score = 0.8

 

#find the z-value with the cumulative probability 80%
#using norm.ppf() ,which is the inverse of norm.cdf()

z_80 = norm.ppf(q_score)

#then transform z value, which is standard normally #distributed to the score conformed to testing score.
z_80_score = z_80 * std_dev + mean


z_80_score

#Result
96.14918220431245

#Alternative way

z_80_score = norm.ppf(q_score, loc = mean, scale = std_dev )

z_80_score

#Result
96.14918220431245

You can also watch full video on Python tutorial from our YouTube channel.